递归面试题

编程题:有n步台阶，一次只能上1步或2步，共有多少种走法?

1.首先从简答的分析。

  • 当 n=1时，只能走一步；当 n=2时，能走两步(一步一步走，一下走两步)

我们这个时候用n表示自变量，用函数F(n)表示n步台阶对应的几种走法。 那么我们就得出。F(1)=1; F(2)=2。

那么当n=3的时候，首先我们第一次可以选择走1步或2步。如果选择走一步的话，那么剩下就是 2个台阶，是不是也就剩下 我们上面分析的F(2)了。反之，我们如果选择第一次走两步，那么剩下的就只有一个台阶了，那就剩下的是F(1)。

用哲学的角度去分析

哲学的自由意志与决定论的辩证,这引发了关于自由选择和决定的思考。

首先，当n=1时，只有一种选择，即走一步，这可以看作是一种决定论的情境，没有自由意志的选择。F(1)=1。

然后，当n=2时，有两种选择，一步一步走或者一下走两步，这展现了一种自由意志的选择。F(2)=2。

随后，当n=3时，我们再次面临选择，可以选择走一步或者走两步。这表现我们在任何时候，先别管自己定义的目标大不大，先尝试做出一个选择。 做完这个选择后可能就后面就一通则通。最起码你想你的目标和调账进行尝试了，不是吗？

这个问题引发了一个递归的思考过程，其中每个选择都导致了更多的选择。更重要的是能走出第一步。这突显了自由意志和决定的相互作用。

总的来说，这个问题反映了哲学中关于自由意志和决定论之间的争论，以及它们如何交织在人类的选择中。

总结分析：

img_2

img_1

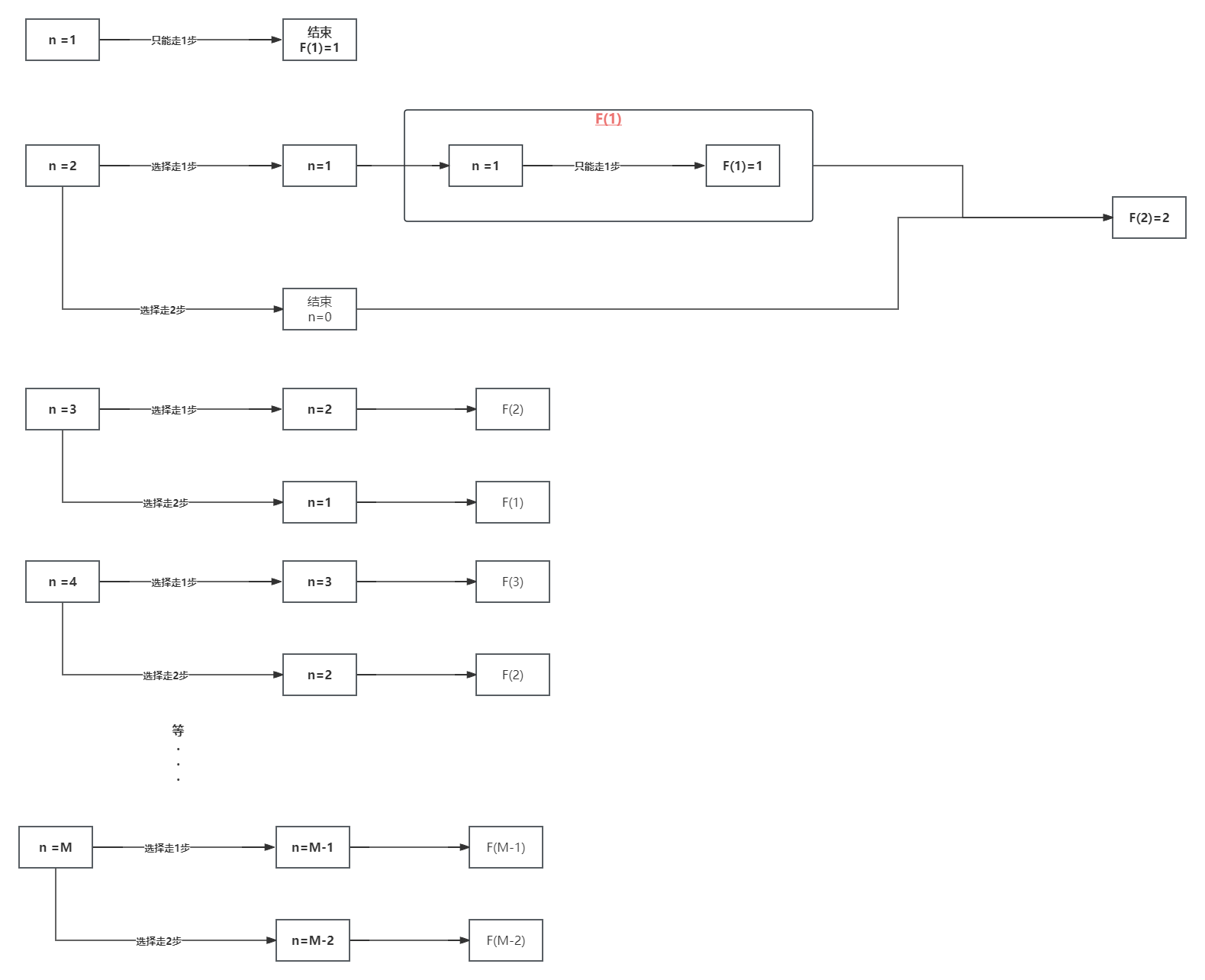
由上图很容易得出，这是个斐波那契数。代码实现的逻辑也是上面展示的效果。

代码实现

FibonacciSequence.java

public class FibonacciSequence {
    /**
     *
     * @param n n步台阶
     * @return 共有多少种走法?
     */
    public static int getNumbers(int n){
        if (n<1){
            throw new IllegalArgumentException(n+"不能小于1啊，大哥！");
        }
        if (n==1||n==2){
            return n;
        }
        return getNumbers(n-1)+getNumbers(n-2);
    }

    public static void main(String[] args) {
        System.out.println("getNumbers(3):"+getNumbers(3));
        System.out.println("getNumbers(4):"+getNumbers(4));
        System.out.println("getNumbers(8):"+getNumbers(8));
        System.out.println("getNumbers(9):"+getNumbers(9));
    }
}